如何编写 PHP 脚本来计算三角形面积

如何编写 PHP 脚本来计算三角形面积

在编程中，计算三角形面积有很多好处。它能帮助你理解逻辑构建和语法，也是学校作业中常见的编程问题。此外，它还有很多实际应用，例如计算机图形学、基于几何的模拟或与构造相关的计算。

在本文中，我们将探讨一个常见问题：给定一个三角形的尺寸，我们的任务是计算它的面积。您可以根据所掌握的三角形信息，使用不同的公式来计算三角形的面积。在这里，您将学习如何使用 PHP 来完成此操作。

阅读本文章后：

• 您将了解计算三角形面积背后的基本逻辑。
• 您将了解如何编写 PHP 代码，使用预定义和用户输入的值来计算三角形的面积。
• 您将了解如何在小型项目和作业中应用此逻辑。

1.先决条件

如果您了解以下几点，您将更容易理解本指南：

PHP 基础

你需要了解基本的 PHP 语法才能完全理解这个问题。如果你知道如何在 PHP 中编写简单的 echo 语句或创建变量，那么你应该可以顺利开始。

本地 PHP 环境

为了成功运行 PHP 代码，您的计算机上应该安装本地 PHP 开发环境，例如 XAMPP 或 WAMP。您也可以使用 PHP Fiddle 或 OnlineGDB 等在线 PHP 编辑器，无需任何安装即可运行 PHP 脚本。

在本教程中，我们将探索三种方法，根据有关三角形的可用信息量来确定 PHP 中三角形的面积。

• 底边和高公式方法：当问题中有底边的垂直高度和底边的长度时，这种方法适用。
• 海伦公式：当知道三角形三边的长度时，这种方法用于计算三角形的面积。
• 三角公式方法：当您知道两条边的长度和它们之间的夹角时，可以应用此方法解决问题。

首先，让我们回到数学课堂并使用一些直接公式来求面积。

2.直接使用公式计算三角形面积

例 1：

在第一个示例中，给定一个三角形的底边和高。你需要返回三角形的面积。在本例中，你将使用直接公式来计算三角形的面积。

输入：

基数 = 5，

高度 = 10

您可以使用以下公式计算三角形的面积：

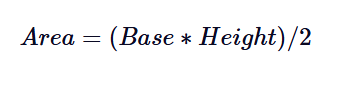
因此，如果您代入您拥有的值，您将得到：（5*10）/2=25。

输出：

面积 = 25

示例 2：

在第二个例子中，给定一个三角形两条边的长度以及它们之间的一个角。你需要计算三角形的面积。在本例中，你将使用另一个直接公式来计算三角形的面积。

输入：

A 边 = 7，B 边 = 9，它们之间的角度 = 60°

在这种情况下，您将使用以下公式：

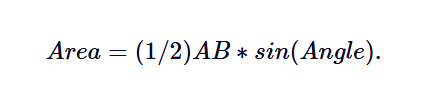
然后只需代入给定的值即可找到面积。

输出：

面积 = 27.33（大约）

现在让我们看看使用 PHP 查找三角形面积的一些不同方法。

3.使用底高法计算三角形面积

当已知底边和高时，这是计算三角形面积最简单、最直接的方法。在这种方法中，您可以直接将数值代入公式，计算出三角形的面积——但您需要使用 PHP 代码来完成。

首先，定义三角形的底和高。然后应用三角形面积公式。如上所述，三角形面积公式为：

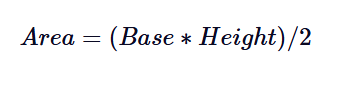
计算出三角形的面积后，输出答案。

好的，下面是我们用 PHP 实现的方法：

<?php
// Define the base and height
$base = 5;
$height = 10;

// Calculate the area
$area = ($base * $height) / 2;

// Output the result
echo "The area of the triangle is: " . $area . " square units.";
?>

输出：

三角形的面积是25平方单位。

在上面的代码中，我们首先用两个变量初始化三角形的底边和高。然后，我们将这些值代入面积公式。PHP 计算三角形的面积并显示结果。

时间复杂度：在上述方法中，我们使用直接公式计算并返回三角形的面积，因此时间复杂度将恒定为 O(1)。恒定时间复杂度是高效的，因为无论底边和高的大小或值如何，它都将保持不变。

空间复杂度：空间复杂度为 O(1)。上述程序使用的空间是恒定的，这确保了最小的内存占用。在优先考虑内存效率的环境中，这种空间复杂度非常理想。

当我们知道三角形的底边和高（无论是直接给出的还是在直角三角形中容易测量的）时，我们会使用上述方法。此方法最适合直角三角形。

4.使用海伦公式计算三角形面积

海伦公式以希腊数学家亚历山大的海伦 (Heron of Alexandria) 的名字命名。当你知道三角形三条边的长度，并且想要计算面积而不需要知道高时，海伦公式非常有用。该公式适用于任何类型的三角形，包括不等边三角形（边长各不相同的三角形）。

这是海伦计算三角形面积的公式：

​

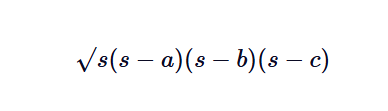
在这里：

• s = 半周长 = (a+b+c)/2 是三角形的半周长。
• a、b、c 分别是边的长度。

首先，我们定义三角形的三条边。然后，我们检验三角不等式定理的所有三个条件。该定理指出，如果两条边之和大于第三条边，则它是一个有效三角形，并且给定的三条边可以构成一个三角形。

我们可以用公式 s = a+b+c/2 计算三角形的半周长。然后，我们可以应用海伦公式计算面积。计算面积后，输出答案。

以下是如何在 PHP 中实现这一点：

<?php
// 定义三角形的边
$a = 7;
$b = 9;
$c = 10;

// 用三角形不等式定理检查这两条边是否构成一个有效的三角形
if (($a + $b > $c) && ($a + $c > $b) && ($b + $c > $a)) {

    // 计算半周长
    $s = ($a + $b + $c) / 2;

    // 用海伦公式计算面积
    $area = sqrt($s * ($s - $a) * ($s - $b) * ($s - $c));

    // Output the result
    echo "The area of the triangle is: " . $area . " square units.";

} else {
    // If the sides can't form a valid triangle
    echo "The given sides do not form a valid triangle.";
}
?>

输出：

三角形的面积为：27.321平方单位。

在上面的代码中，我们首先创建三个变量来存储三角形的边长，并利用三角不等式定理检查给定的边是否构成一个有效的三角形。然后，我们使用公式 s = a + b + c / 2 计算半周长。我们将半周长的值和所有边长代入海伦公式中计算面积。使用公式计算后，返回三角形的面积。

时间复杂度：加法、减法、乘法和平方根等运算的总数是固定的。这些运算与输入大小无关，因为它们只执行固定次数。这意味着时间复杂度为常数 O(1)。

空间复杂度：我们使用固定数量的变量来计算三角形的面积。我们没有使用任何其他数据结构，例如数组或对象。程序中的内存使用量是恒定的，这更适合低内存环境。空间复杂度为常数 O(1)。

当所有边的长度都已知时，这种方法效果最佳。这种方法主要用于不等边三角形或等腰三角形，因为这些三角形的高度无法直接给出。然而，这种方法适用于任何类型的三角形——不等边三角形、等腰三角形或等边三角形。

5.使用两条边和夹角计算三角形面积（三角公式）

在这种方法中，我们将看到问题的不同变体。当你知道三角形的两条边以及它们之间的夹角时，你可以使用以下公式计算面积：

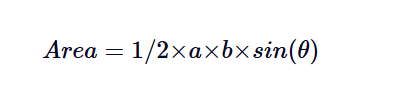
在哪里：

• a 和 b 是两条边的长度。
• θ 是两边之间的夹角，以度或弧度为单位。

使用上述公式，无需知道三角形的高度即可计算其面积。首先，定义三角形的两条边以及它们之间的夹角。然后，如果需要，将角度从度转换为弧度（在 PHP 中，可以使用 deg2rad() 将度转换为弧度）。最后，应用公式即可。

计算出三角形的面积后，输出结果。

以下是如何在 PHP 中实现这一点：

<?php
// 确定两边和夹角
$a = 7;
$b = 9;
$angle = 60; // Angle in degrees

// 把角度从度换算成弧度
$angle_in_radians = deg2rad($angle);

// 用公式计算面积
$area = 0.5 * $a * $b * sin($angle_in_radians);

// Output the result
echo "The area of the triangle is: " . $area . " square units.";
?>

输出：

三角形的面积为：27.321平方单位。

解释：

在上面的例子中，我们使用以下公式：

三角形面积 = 1/2 × a × b × sin(θ)

我们将以下值代入公式中：

面积= 1/2 × 7 × 9 × sin(60 ∘) ≈ 27.321

在代码中，我们声明了两个变量来存储三角形两边的长度，变量$angle保存夹角（以度为单位）。我们使用了deg2rad()PHP 内置函数 ，该函数可以将角度从度转换为弧度。然后，我们应用了实际公式：面积 = 1/2 × 7 × 9 × sin(60 ∘)。PHP 将最终答案存储在变量 中$area。

时间复杂度：当给定两条边的长度和它们之间的角度时，我们使用直接公式来计算三角形的面积。恒定时间复杂度为 O(1)。

空间复杂度：同样，它不占用任何额外空间或使用任何数据结构。它使用单个变量来存储结果，因此空间复杂度为常数 O(1)。

这种方法非常适合已知两条边和夹角（这两条边之间的夹角）的问题。当你无法轻松计算三角形的高时，可以使用这种方法。这类问题在实际生活中的几何问题、CAD 应用或物理模拟中都有应用。这种方法非常精确，并且不需要知道所有边的长度。

6.结论

在本文中，您学习了如何手动计算三角形的面积以及使用 PHP 计算。您了解了不同的计算方法，并根据现有信息了解了哪种方法最合适。首先，我们讨论了底和高法，然后研究了海伦公式，最后研究了当已知两条边和夹角时如何处理。

了解每种方法背后的逻辑有助于您根据给定的数据选择正确的方法。